0.5mで300円のリボンは、1mでいくら？

 

 

この式は、300÷0.5でいいのでしょうか？

 

それとも、300×2でいいのでしょうか？

 

もちろん、答えはどちらも同じになります。

 

さぁ、算数を『意味で考える』授業の始まりです！

 

 

先ほどの問題を深く考えていく前に、

 

以下の問題を解いてみましょう。

 

 

これらの式は、おそらく皆さん同じだと思います。

 

１）が、300÷4 となりの、

 

２）が、300÷15 となったのではないでしょうか？

 

 

では、なぜ冒頭の問題には、

 

２つの式が生まれてくるのでしょう？

 

もしかすると、300×2の方が多いかもしれませんね。

 

では、300円にかけた「２」という数字は

 

どこから出てきたのでしょうか？

 

もちろん、1m分の金額を求めたいので

 

1mは0.5mの「２倍」です。

 

ですから、0.5mで300円のリボンの

 

「２倍」分を求めたいから出来た式が

 

300[円]×2[倍]=600[円]　となる訳ですね。

 

 

 

では、

 

300÷4 / 300÷15 / 300÷0.5　の

 

式で使っている割り算はどのような意味で

 

使っているのでしょうか？

 

このように考えてみましょう！

 

 

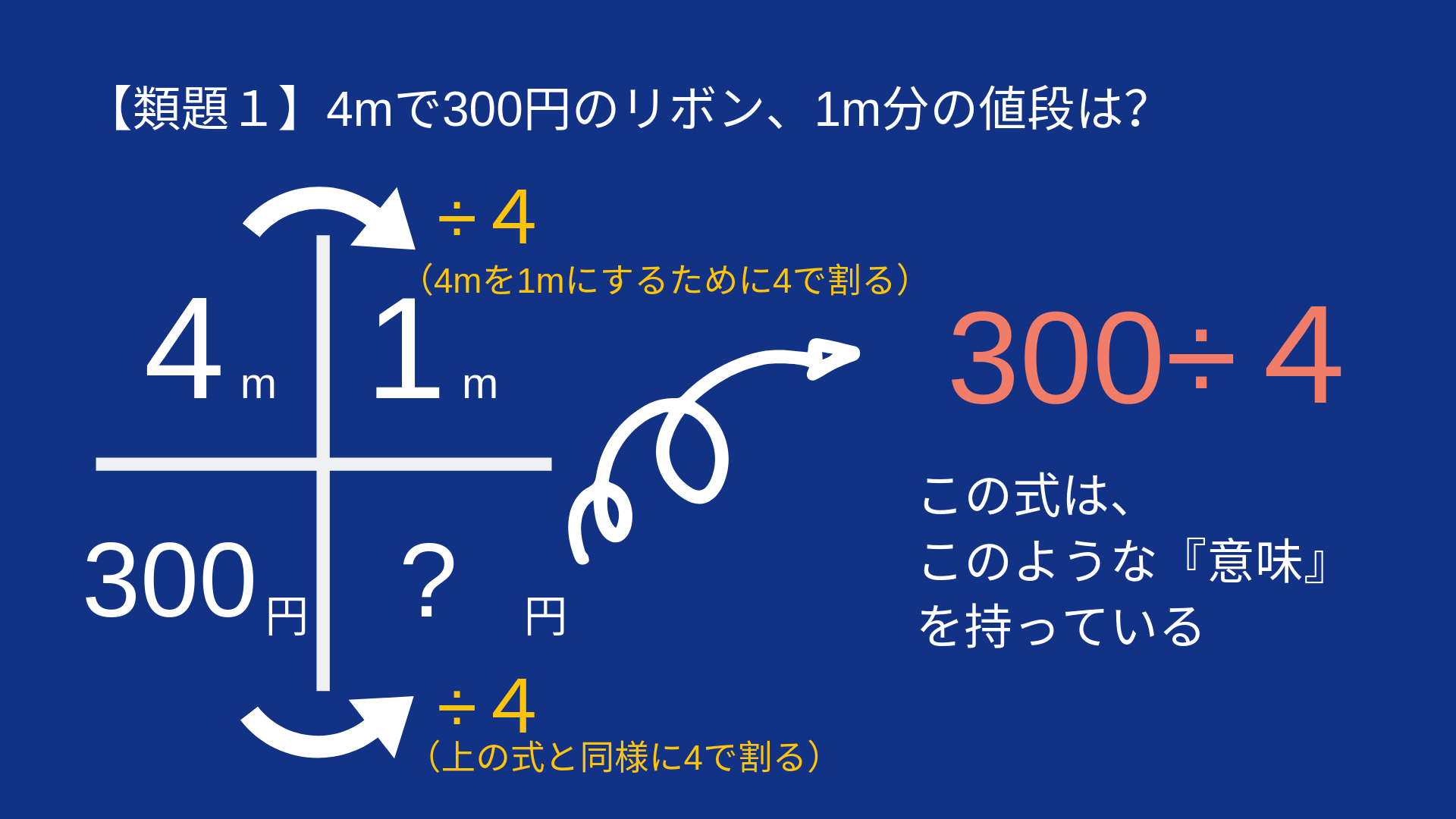
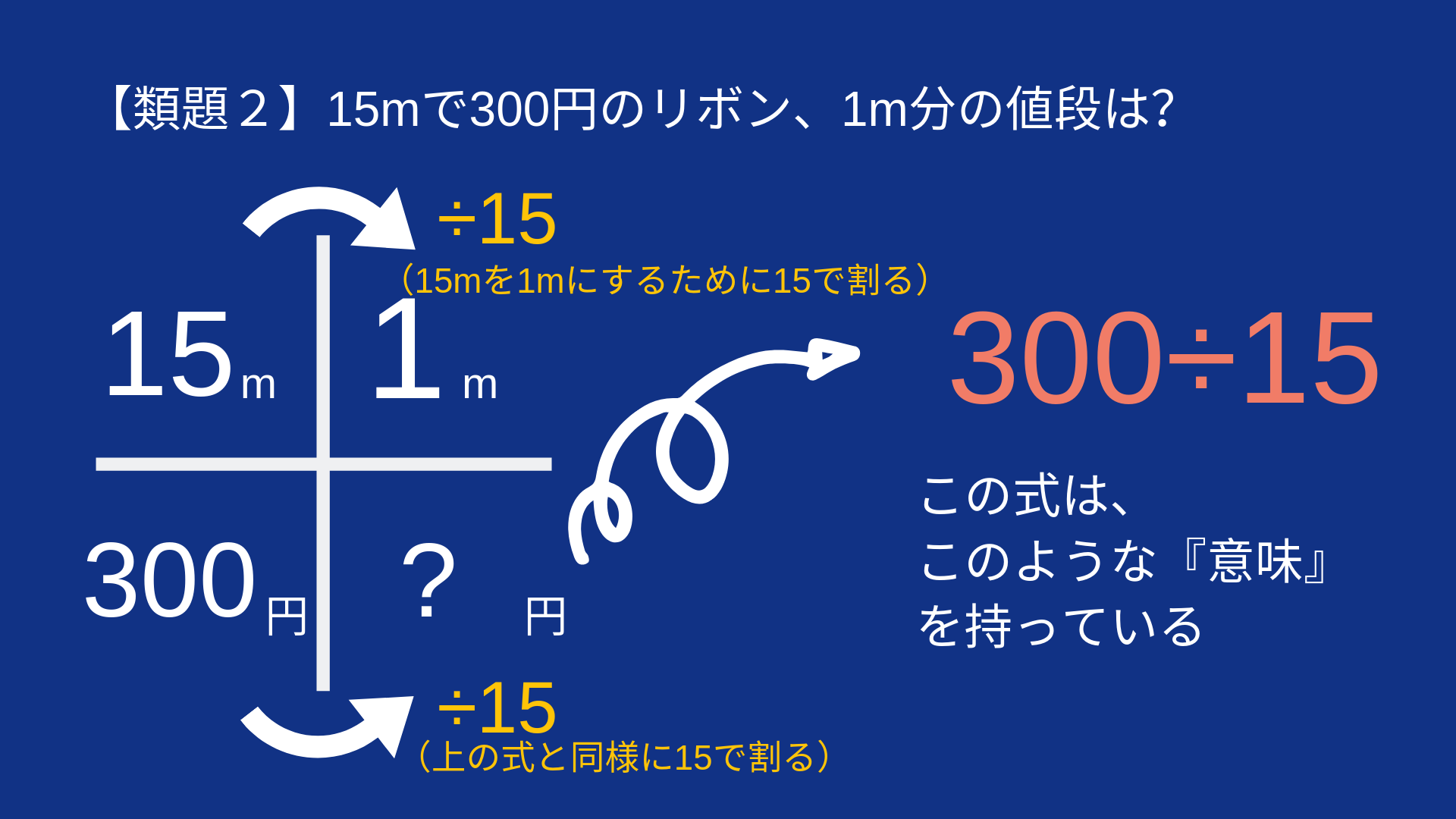
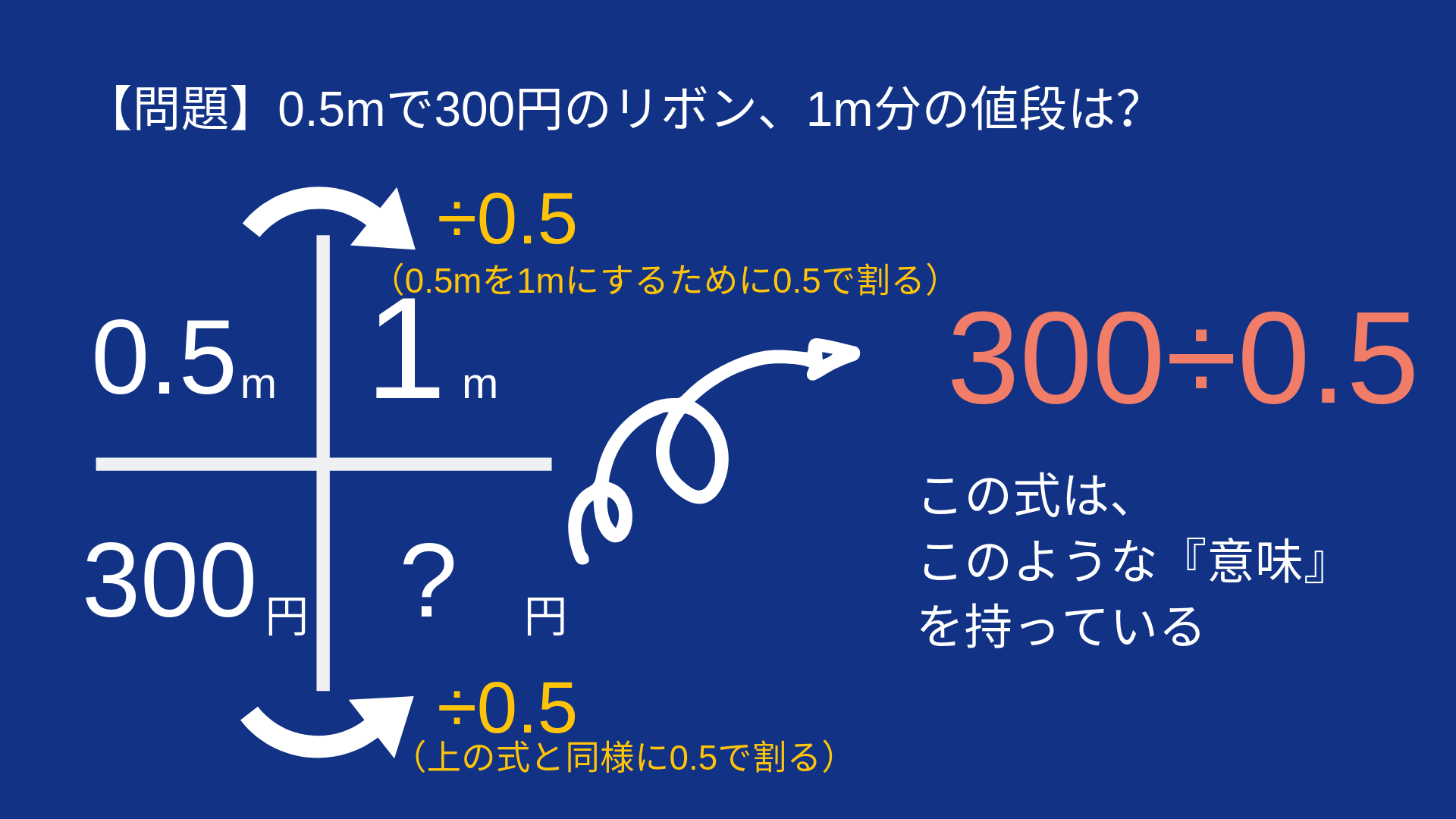
このように考えると、

 

÷4、÷15、÷0.5の「意味」が見えてきます。

 

これらは、

 

÷4[m]、÷15[m]、÷0.5[m]という意味ではなく

 

1m分を求めたいから、

 

元の長さと同じ数字を割っただけなのです。

 

これが分かり出すと、次のような問題も

 

楽々わかるようになってしまいます。

 

 

もう、あっという間に式が思い浮かびましたね？

 

0.18mを1m分にするために、

 

同じ数で割ってあげればいいだけなのです。

 

よって、

 

360÷0.18=2000[円]

 

となる訳ですね。

 

 

 

算数を「意味」で考えること。

 

これは文章や式がどのような

 

「意味」であるかを考えることです。

 

 

願わくば、私もこんな算数を

 

習って小学校を過ごしてみたかったです（笑）

 

ちゃん♪ちゃん♫